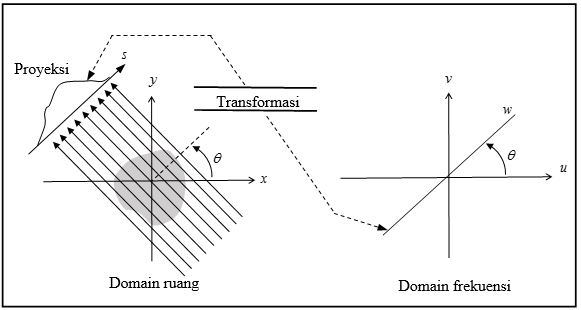
Sesuai dengan namanya, metode rekonstruksi filtered back projection terdiri dari dua
proses pokok yaitu pemfilteran dan proyeksi balik. Proyeksi balik
merepresentasikan akumulasi penjumlahan sinar yang melewati suatu titik (x,y).
Persamaan invers
transformasi Fourier dua dimensi dirumuskan dengan (Pers. 1) :
Pengubahan koordinat katresian pada domain frekuensi, (u,v) menjadi sistem koordinat polar untuk berkas paralel dapat dilakukan dengan beberapa hubungan berikut (Pers. 2):
Sehingga bentuk differensial dudv berubah menjadi (Pers. 3):
(Pers. 1) akan menjadi (Pers. 4):
Bentuk integral ini dapat dipisah menjadi dua bagian berdasarkan nilai teta 0˚ sampai 180˚ dan 180˚ sampai
360˚ (Pers. 5).
Dengan menggunakan sifat :
(Pers. 5) dapat dituliskan menjadi (Pers.6) :
dengan menyederhanakan bentuk
Apabila transformasi Fourier satu dimensi dari sebuah proyeksi pada
sudut teta dinyatakan dengan Steta(w) , maka sesuai dengan teorema irisan Fourier Pers.6 dapat dituliskan menjadi :
Dalam penulisan yang lebih singkat, dapat
dituliskan :
Nilai f(x,y) pada persamaan memiliki bentuk yang lebih sederhana yang didalamnya terdapat nilai
transformasi Fourier data proyeksi. Pers. 7 merepresentasikan adanya operasi penapisan (filtering) dengan respon
frekuensi dari filter diberikan oleh |w|. Sehingga persamaan
disebut sebagai “proyeksi
terfilter” yang dilakukan terhadap data proyeksi. Hasil proyeksi untuk sudut teta yang berbeda kemudian dijumlahkan
untuk membentuk nilai estimasi total dari f(x,y) (Kak dan Slaney, 1998).